AE教程！教你用表达式制作病毒落水弹跳动画

教程作者：Hicyy（授权转载）

交作业：#优设每日作业#

“从视觉效果出发，向设计师朋友们介绍如何通过表达式而不需要手动K帧的方式来实现真实细腻的病毒落水弹跳动画。”对于AE表达式只掌握了“砍臭C砍臭V”的核心用法的旁友，如果怕被表达式背后的故事劝退，那把以下这段带走就好了：

amp=0.1;
freq=10;
decay=2;
a=numKeys;
n=nearestKey(time).index;
et=key(n).time;
t=time-et;
v=velocityAtTime(et-0.01);
if  (t>0 & n>=a){
    value+v*amp*Math.sin(t*freq)/Math.exp(t*decay);
}
else{
    value;
}

前言

这是一篇非编程向、数学向、物理向的技术探讨小文，一切从视觉效果出发，向设计师朋友们介绍如何通过表达式，而不需要手动K帧的方式，来实现真实细腻的病毒落水弹跳动画。

请编程高手、数学课代表，物理老师自觉忽略其中不科学、不正统的细节，同时有好的方法也希望不吝赐教，至于我能不能看懂就随缘吧。

正文

疫情开始之后便再没了“阳光明媚的下午”，因为不论窗外再晴朗，心里面总会有一小片乌云，它让人焦灼、压抑，为着那些未知的风险，为着这场猝不及防的危机，还有那些甚至为此失去生命的人们。

它何时才能结束呢？此时我是多么想岁月静好！也大概是因为疫情，让我越发觉得想好的事情就应该尽快去做，毕竟不知道明天和意外谁先来，立的flag也许拖着拖着就很意外地忘了呢。

所以这次的表达式动画以冠状病毒为主角，分3个场景用3个表达式做3个动画，剧情是病毒的3种死法，祈愿病毒快点消失。

本文是第1种死法———病毒落水而死。先来看看效果：

*病毒落水的弹跳，水位上升的弹跳均用了同一段表达式

原先我打算在烧杯里倒入双黄连溶液，但双黄连兽用的都被抢光了，不得已把颜色改成了淡淡的蓝。接下来，才是真的正文，表达式的基本概念在上一篇中已经讲过了，从零开始学的旁友应该先看看上一篇，如果只是从零开始复制粘贴的话那当我没写过上一篇。

真的正文

一、函数释义

numKeys：关键帧的数量，返回值是一个整数，比如你在某属性上打了两个关键帧，该属性下的numKeys=2。

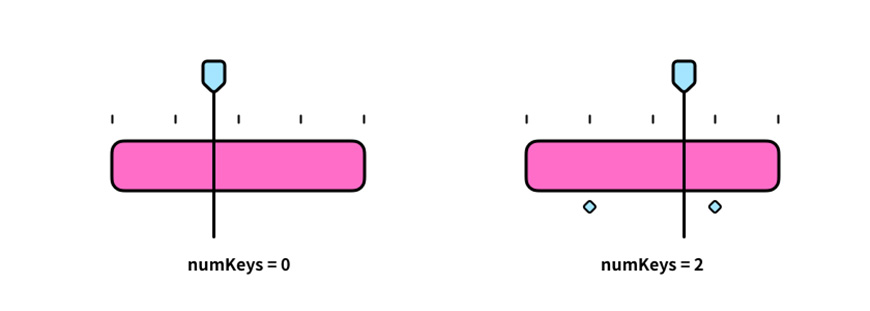
nearestKey(time).index：先翻译下，“最近的关键帧（时间）.索引”，“.”在函数里通常可以翻译成“的”，脑补一下就是“离时间线指针最近的关键帧的的索引（序号）”，返回值是一个整数。

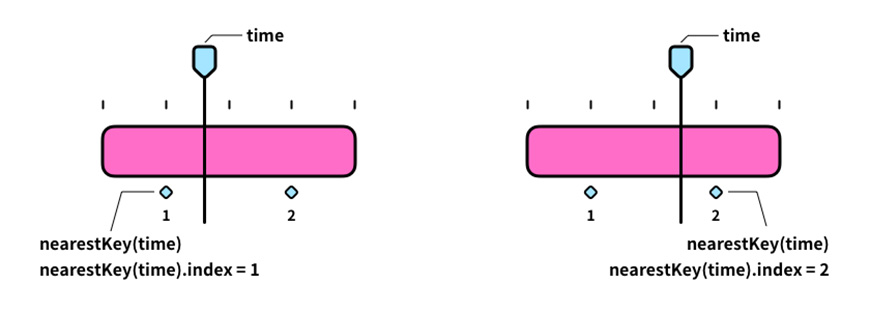
key(n).time：第n个关键帧所在的时间，输入n的值，输出时间的值，单位默认是秒。比如在一个属性中，打下两个关键帧，第2个关键帧所在的时间是3秒，key(2).time=3。

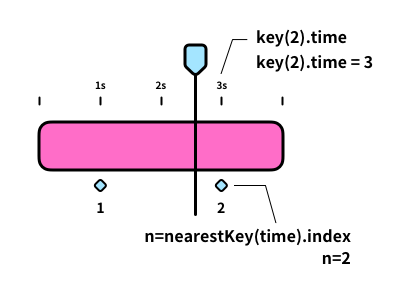
velocityAtTime：在某时的速度，这句几乎不需要想象力。

二、网传版表达式

我们来看一段在网上流传的表达式，原作者貌似是一位国外的大神，这段表达式也是我研究弹性表达式的一个契机。网上也有其他设计师对这段表达式的解读，但由于这段表达式的逻辑本身有点绕（也可能是我的脑回路并不适合研究代码），那些解读基本都没有讲太清楚。

而本文除了要再次尝试把它的逻辑理顺之外，还重写了更简单但效果几乎一样的表达式，对于想要了解表达式的旁友来说，我重写的版本可能更容易理解，对于复制粘贴的旁友来说那差别不大。

先把原表达式奉上：

amp = .1;
freq = 2.0;
decay = 2.0;
n = 0;
if (numKeys > 0){
n = nearestKey(time).index;
if (key(n).time > time){n--;}
}
if (n == 0){ t = 0;}
else{t = time - key(n).time;}
if (n > 0){
v = velocityAtTime(key(n).time - thisComp.frameDuration/10);
value + v*amp*Math.sin(freq*t*2*Math.PI)/Math.exp(decay*t);
}
else{value}

变量释义：

amp = .1; //定义一个叫amp（振幅）的变量，赋值0.1

freq = 2.0; //定义一个叫freq（频率）的变量，赋值2.0

decay = 2.0; //定义一个叫decay（衰减）的变量，赋值2.0

n = 0; //定义一个叫n的变量，初始值为0，具体用来干嘛，继续往下看

n = nearestKey(time).index; //马上就告诉你，n默认表示离时间线最近的关键帧的序号，本质是一个数字

t = time - key(n).time；//t是时间线与某个关键帧所在时间的差值

thisComp.frameDuration/10 //此合成帧时长的十分之一，如果一个合成共100帧，时长5秒，则thisComp.frameDuration/10=5/100/10=0.005

v = velocityAtTime(key(n).time - thisComp.frameDuration/10); //还用上一句注释中的例子，v就表示在某序号为n的关键帧前0.005秒时的速度

value + v*amp*Math.sin(freq*t*2*Math.PI)/Math.exp(decay*t); //

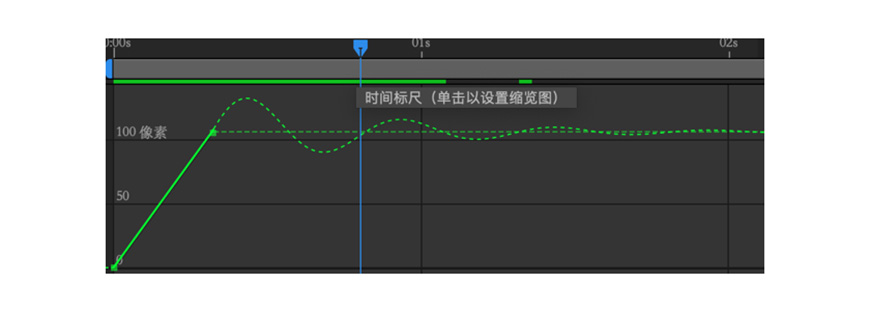
属性值+弹性表达式运算生成曲线所对应的值，如下图中，绿色实线就是属性值，是两个关键帧之间的值，绿色波浪形虚线则是表达式运算生成的部分。

其中v、amp与弹跳的幅度（波浪线波峰波谷的高度差）正相关，v、amp值越大，波浪线浪越高，弹跳幅度越大；freq与波浪线的频率（两个波峰的间距）正相关，freq值越大，出现波峰的频率越高，波峰间的间距越小，浪越急，弹跳速度越快；PI就是那个π，就是3.141592654…换个别的数也行，只是这么写看上去数学成绩更好一点；decay值越大，衰减速度越快，也就是波越快变平，弹性越容易消失。

正弦函数（三角函数）的工作原理在我的上一篇《从零开始做AE表达式动画之——铃铛摆动动画》中已经做了粗浅讲解，深入讲解可以参看高中数学。

在这里我还要补充说的是，前文中为什么将amp的值定为0.1，freq的值定义为2呢？

这里面其实并没有什么科学道理，看到下图中笔直的实线跟扭曲的虚线了吗，虚线的开端延续了实线的坡度，它们是不是衔接得浑然一体，宛如被人工雕琢过的？

没错，我就是那个人工！所以定义成那几个值就是为了这个完美的衔接，反映在动画上就是关键帧动画走完之后到弹性动画部分过渡流畅自然无跳跃感。至于那0.1和2为什么是“天选之值”，你数学成绩好你来作答！

流程解析

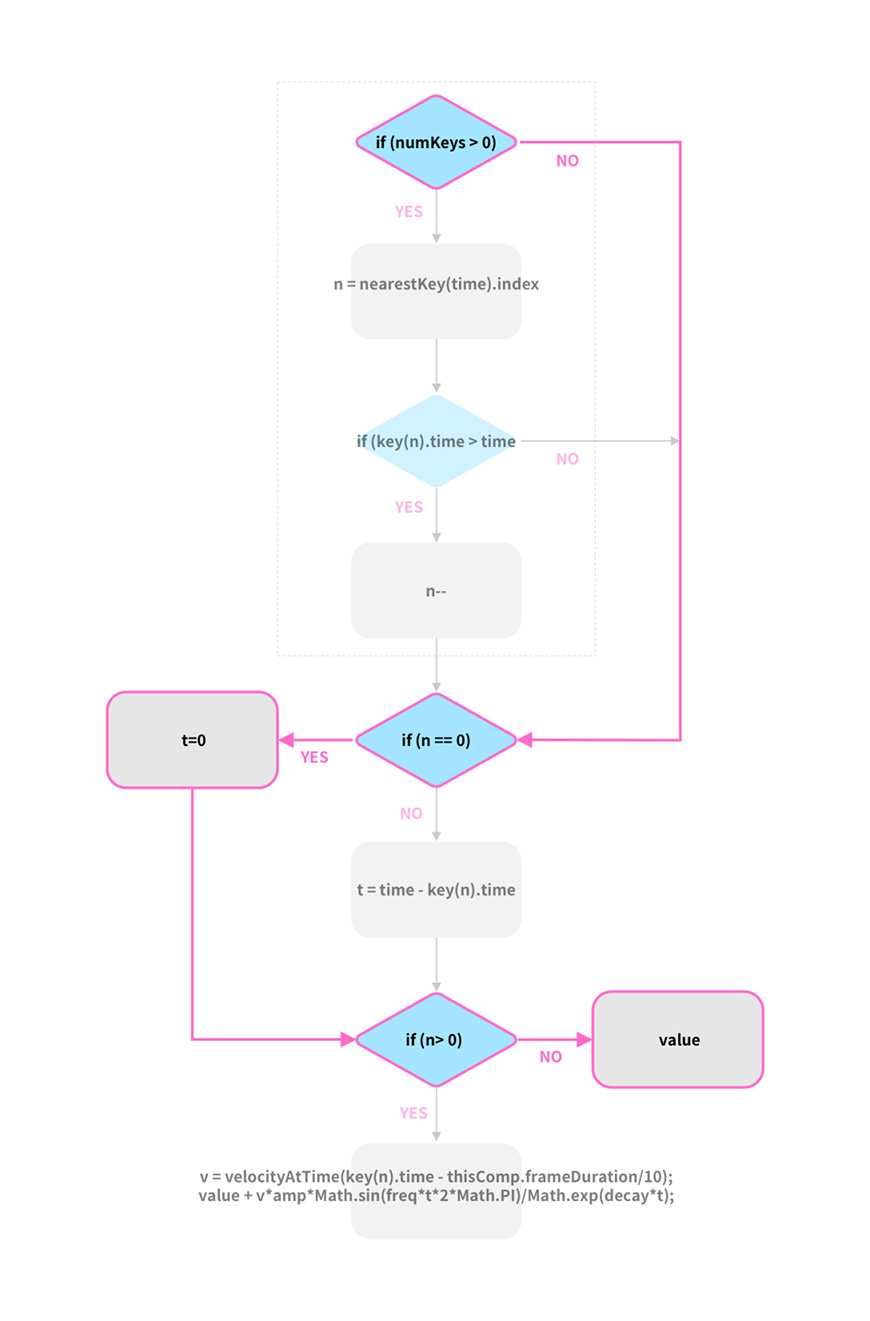
So，将表达式梳理成流程图之后如下：

我们来看看，当关键帧数量不同时，时间线所在位置不同时，表达式是如何工作的。

1. 当无关键帧时，numKeys=0，开始判断n是否为0，在一开始的定义中，n=0，故最后t=0，n当然也不大于0，最后执行value值，也就是属性本身的值。流程走向如下图高亮部分：

2.1 当numKey=1的时候，如下图情形，有一个关键帧，时间线在关键帧之前或者之后。当时间线在关键帧之前时，key(1).time>time,n—(即n=n-1)，n=1-1=0,所以t=0…最后执行value。

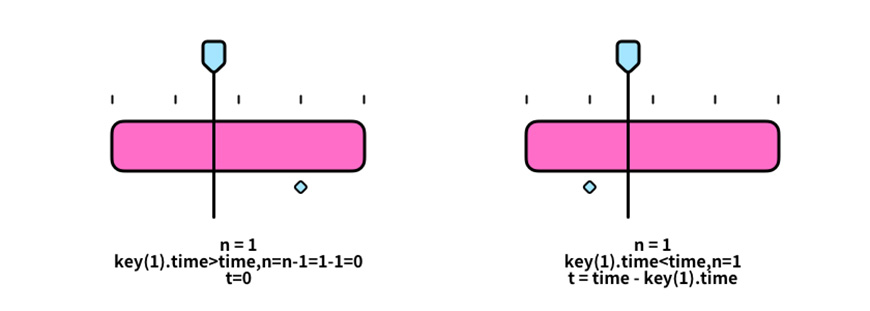
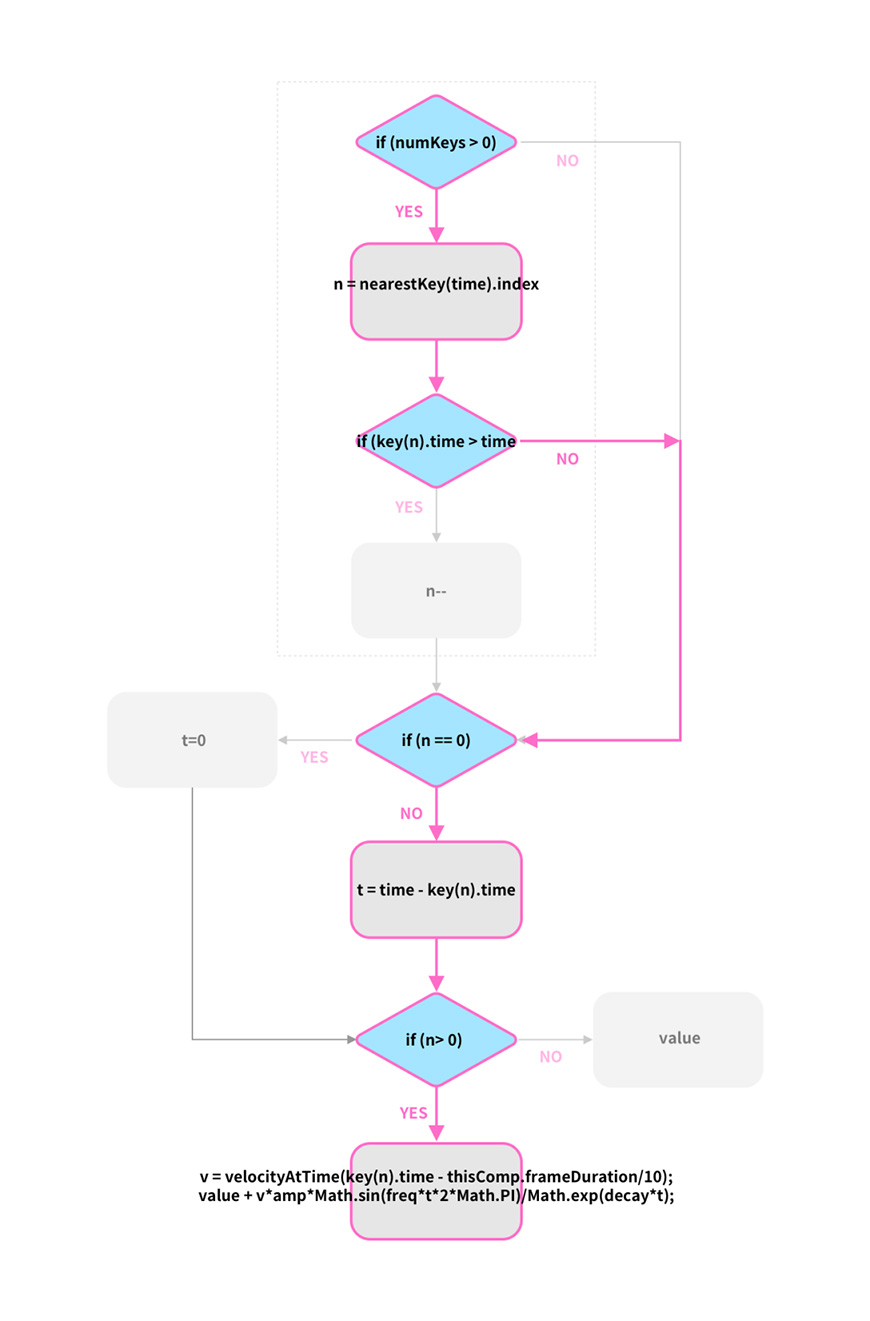
2.2 当时间线在关键帧之后时，key(1).time<time,且n不等于0，得到了时间线与关键帧的差值t，并参与了最后弹性曲线的运算：

“v = velocityAtTime(key(1).time - thisComp.frameDuration/10);

value + v*amp*Math.sin(freq*t*2*Math.PI)/Math.exp(decay*t);“

但不幸的是，关键帧前的瞬时速度v为0，因为关键帧前的value值并没有产生变化，所以不会有速度，因此“value + v*amp*Math.sin(freq*t*2*Math.PI)/Math.exp(decay*t);“等价于”value+0“，最后执行的仍然是value值。流程如下：

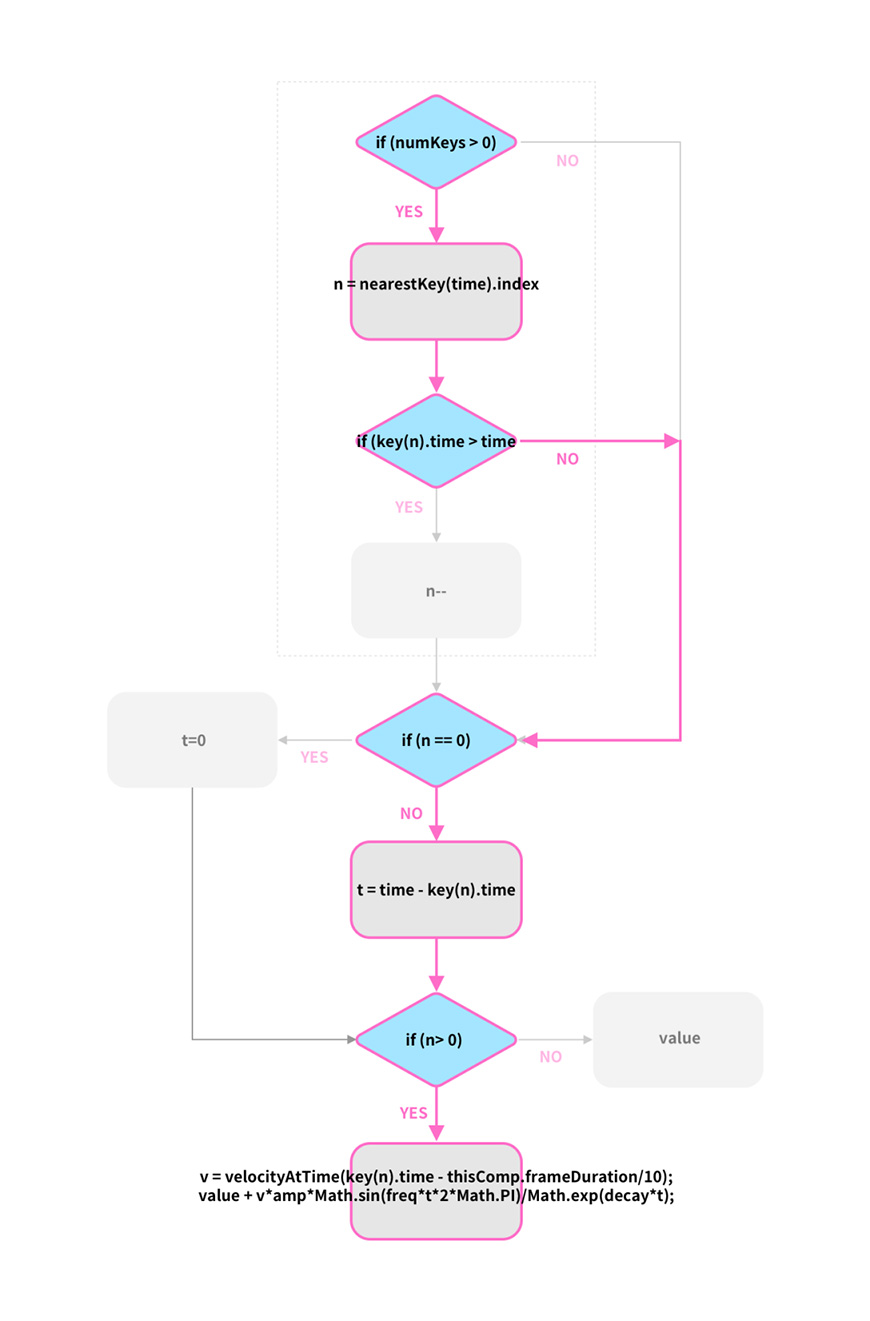
3. 在本文病毒落水的动画中，关键帧数量为2，即numKey=2，时间线的位置有以下几种可能:

• A.位于第一个关键帧之前（key(1).time>time,n=n-1）
• B.位于两个关键帧之间但离第一个更近（key(1).time<time）
• C.位于两个关键帧之间但离第二个更近（key(2).time>time,n=n-1）
• D.位于第二个关键帧后面(key(2).time<time）

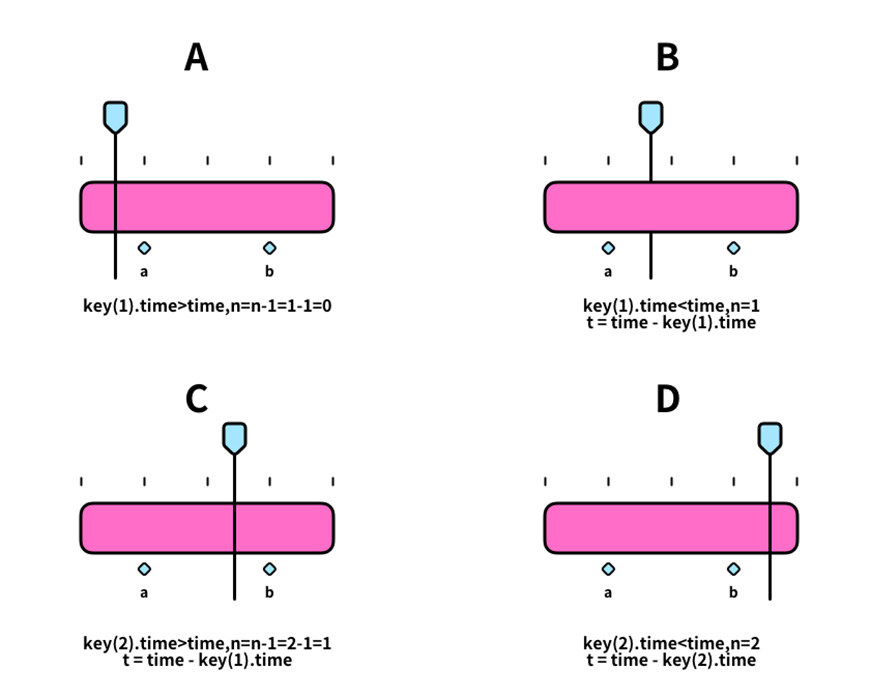
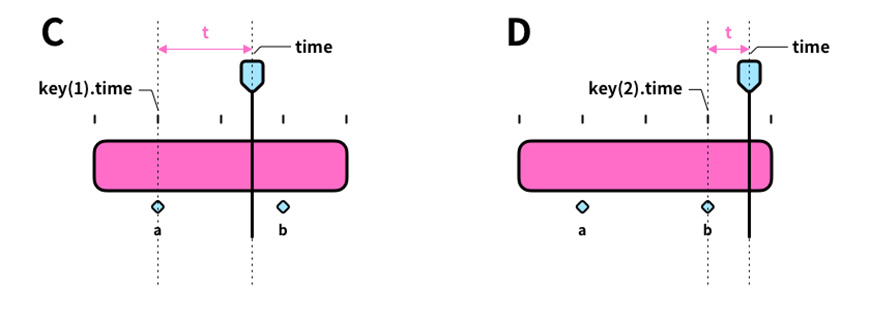
对照流程图，A、B两种情形分别同前文中 2.1、2.2 中的流程走向。C情形下得到的t值是时间线与关键帧a所在时间的时间差，D情形下得到的t值是时间线与关键帧b所在时间的时间差。并且最后都参与弹性曲线部分的运算，D情形下弹性曲线以b为起点，C情形下弹性曲线以a为起点。

但为何在AE的表达式图表中体现了D情形下的弹性曲线，却没有体现C情形下的曲线部分呢？如下图：

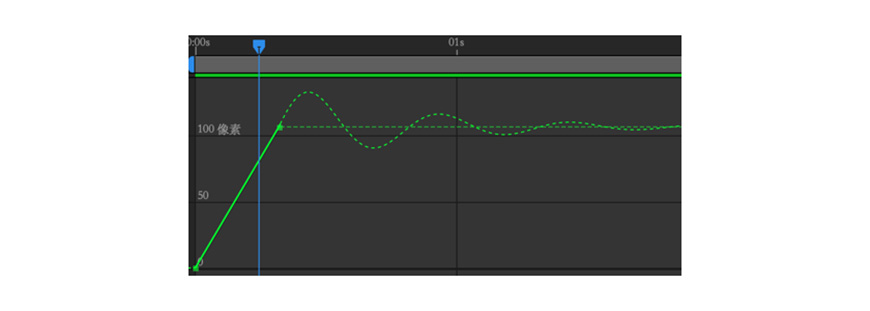
因为C情形下，关键帧a作为第一个关键帧，帧前的瞬时速度v同样是0，弹性曲线“value + v*amp*Math.sin(freq*t*2*Math.PI)/Math.exp(decay*t)”得到的值同样等价于value，所以表达式在第一个关键帧后面注定不会产生曲线。

通过流程图进行推演，当关键帧有三个甚至更多时，也会在除第一个关键帧之后的全部关键帧后面产生曲线。如下图：

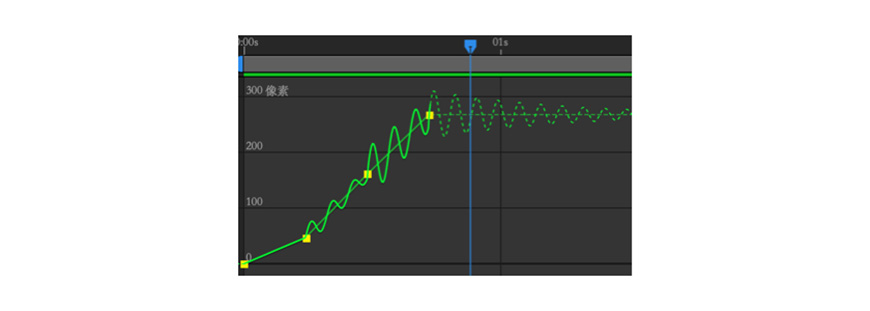
但通常来说，我们并不需要在对多个关键帧之间产生弹性曲线来做弹跳补间，大多数时候我们只需把弹性加在某个属性运动的末尾，所以就有了我接下来的简化版本，只为了表达式更好理解，也在保证功能的基础上看上去更简洁，发量稀疏的旁友可以只看以下版本。

三、简化版表达式

妈呀，终于写到这里了，我也差不多要死了，写那么多也许压根就没人看，看到了这句你就吱个声。

简化版之一：

amp = .1;
freq = 2.0;
decay = 2.0;
n = 0;
if (numKeys > 0){
n = nearestKey(time).index;
if (key(n).time > time){n--;}
if (n <= 0){value}
else{
t = time - key(n).time;
v = velocityAtTime(key(n).time - thisComp.frameDuration/10);
value + v*amp*Math.sin(freq*t*2*Math.PI)/Math.exp(decay*t);}
}
else{value}

流程图如下：

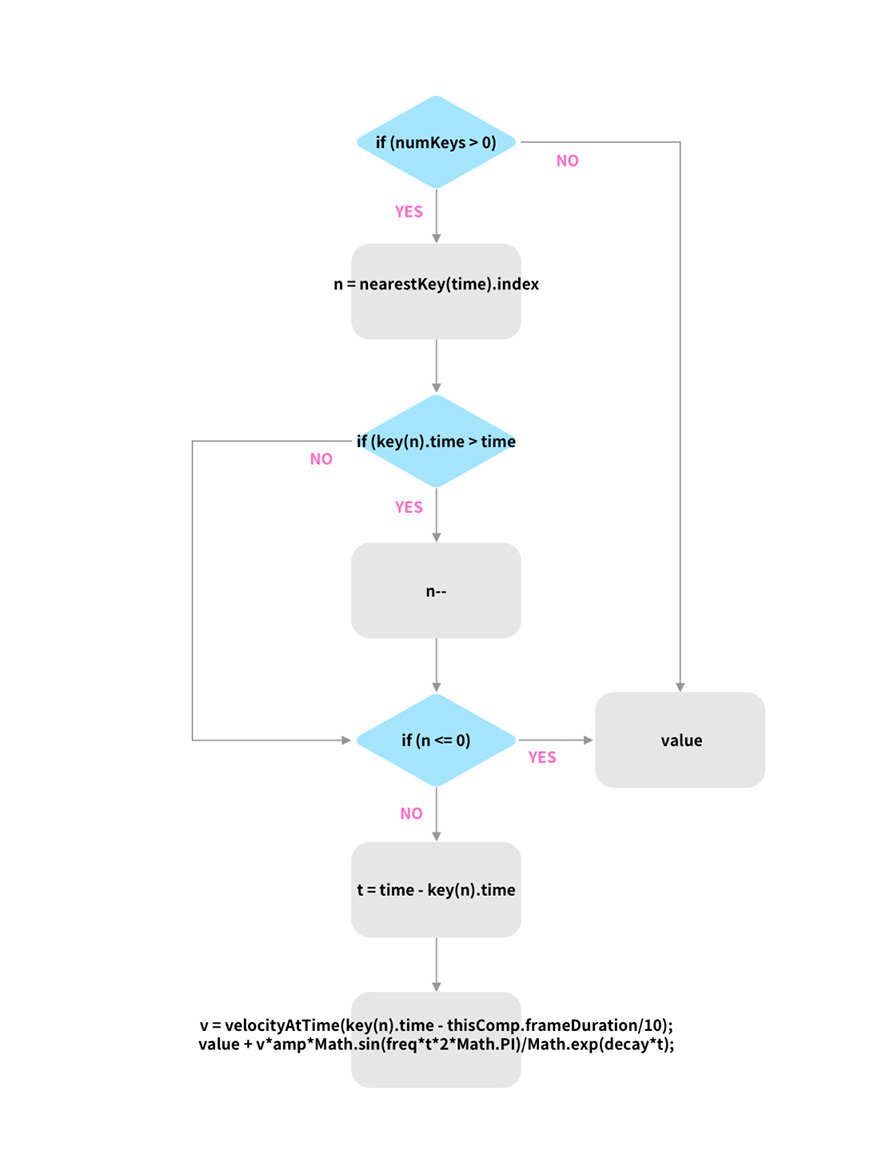
对比原版可以看出，减少了一个条件判断，达到了一模一样的效果，理解起来更简单了，不管你n是否大于0，只要小于或等于0，即说明当前离时间线最近的关键帧是第一个关键帧，且时间线在它前面，这种情况下只有一条路，乖乖走value值。

如果其他情形下，不管时间线在两个关键帧之间还是之后，通通都会参与弹性曲线运算，区别只在于，时间线在头两个关键帧之间时，也就是第一个关键帧之后，第二个关键帧之前时，n到最后都等于1，t都是时间线与第一个关键帧所在时间的差值，但都因为第一个关键帧前的瞬时速度v为0，导致最后的运算结果依然只是value。不知道出于什么原因原作者要搞这么复杂，可能真的就是为了让人头秃吧。

简化版之二（作者推荐版）

没错，还有第二版，是我重新写的，高亮加粗显示，ctrl+c，ctrl+v的请关注这里：

amp=0.1;
freq=10;
decay=2;
a=numKeys;
n=nearestKey(time).index;
et=key(n).time;
t=time-et;
v=velocityAtTime(et-0.01);
if (t>0 & n>=a){
value+v*amp*Math.sin(t*freq)/Math.exp(t*decay);
}
else{
value;
}

定义完变量之后，只做了一次条件判断，就开始抄家伙干活了。

“if (t>0 & n>=a){
value+v*amp*Math.sin(t*freq)/Math.exp(t*decay);
}”

t>0即时间线在离它最近的关键帧后面；且n>=a,即n大于关键帧的总个数；当两个条件均满足的时候，表示时间线在最后一个关键帧后面，此时开始绘制弹性曲线，否则就走value值。是不是非常简单，非常直接，非常清爽？简单到画流程图都是多余！我只是想在动画的末尾加上一丢丢弹性啊，这样就很完美了不是么？

如果说还有润色的余地，那就是把decay的值与v进行关联,实现下落速度越快，衰减越慢、弹跳越久，这样会更符合物理世界的规律，具体怎么关联就交给大家去想吧，需要用到的只是小学数学，或者就等我的下一篇《从零开始学做表达式动画之——病毒落地弹跳动画》，嘿嘿嘿～

最后的话

最后再奉上几个动画，它们均用到了本文中的弹性表达式（以及下一篇要讲的表达式）。老规矩，获取源文件可关注作者公众号获取。

病毒无情，人间有爱，希望大家都能安好。

*压制必反弹

*脱离根基，如何不倒？

想要来「优优交流群」和其他小伙伴一起学习分享吗？搜索 QQ 群：1078133504 进群暗号：优优的忠实观众

学完这篇教程的人还在学…